The Graceful Tree Conjecture: A Major Unsolved Problem in Mathematics
A little game
One of the major open problems in graph theory is the graceful tree conjecture also known as Ringel-Kotzig conjecture. The conjecture is remarkably simple to state:
"All trees are graceful".
Despite its simplicity, this statement has remained unproven since it was proposed in 1967. To this day, we have neither a general proof nor a counterexample.
Before getting into the formal definitions of trees and graceful labelings, let's start with a small puzzle.
A puzzle
You are given 6 circles connected by lines as follows:
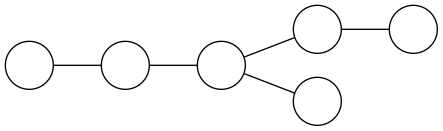
Your task is to fill the circles with the numbers 1 through 6, such that:
- Each circle contains a distinct number from 1 to 6
- Each line (edge) is labeled with the absolute difference of the numbers in the two circles it connects
- All edge labels are distinct
For example

Here, the circles are labeled 5 and 3, and the connecting line is labeled 2 since |5 − 3| = 2.
The goal of the game is to assign numbers to the circles so that:
- All vertex labels are unique
- All edge labels are unique
You can stop here and try to solve the puzzle yourself before reading on.
A solution
One possible solution is:
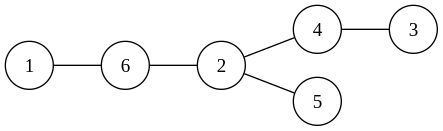
Labeling the edges gives:
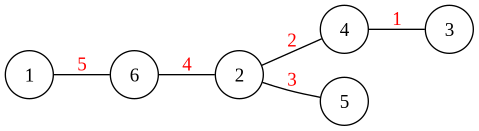
All edge labels are distinct and cover the values 1 through 5 exactly once.
This type of labeling is called a graceful labeling.
In graph theory terminology:
- A set of circles connected by lines is called a graph
- A connected graph with no cycles is called a tree
So congratulations! By solving this puzzle, you have just shown that this particular tree with 6 vertices is graceful.
The real question is:
Can this be done for every possible tree?
That is precisely the graceful tree conjecture.
Definitions
A graceful labeling of a graph with \( n \) edges is an assignment of labels such that:
- Each vertex receives a distinct integer label from \( \{0, 1, 2, \dots, n\} \)
- Each edge is labeled with the absolute difference of its endpoint labels
- The resulting edge labels are exactly \( \{1, 2, \dots, n\} \), each appearing once
A tree is a graph in which every pair of distinct vertices is connected by exactly one simple path. Equivalently, it is a connected graph with no cycles.
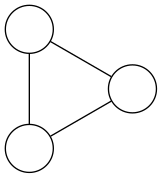
Examples of graphs with cycles (i.e., not trees):
The Ringel–Kotzig Conjecture
Every tree admits a graceful labeling.
Despite decades of research, this conjecture remains open.
Selected Results
Although the conjecture is still unresolved in full generality, it has been proven for many important classes of trees.
All paths are graceful
Consider the following path-like tree:
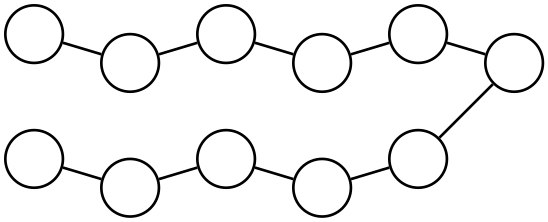
We label the vertices clockwise, assigning increasing numbers while skipping one vertex at each step.
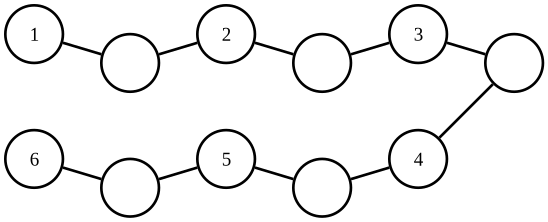
Continuing from the last vertex and filling in the remaining labels yields a graceful labeling:
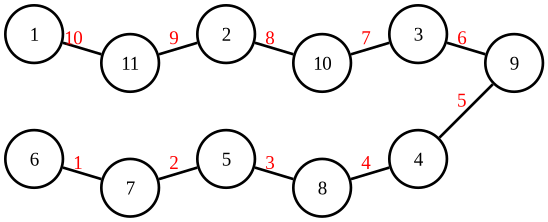
Proven for many other families
- Symmetrical trees [Bermond & Schonheim 1977]
- Spider trees [Bahls, Lake & Wertheim 2010]
- Lobster trees [Morgan 2002]
- Firecrackers [Chen et al. 1997]
- Bamboo trees [Ramachandran & Sekar 2014]
- Coconut trees [Ramachanfra & Sekar 2014]
Recommendation
This is a new segment where, in each article, I'll share an educational resource I find genuinely valuable.
Today I would like to share with you an amazing piece of the internet, strudel, a live coding platform to write dynamic music pieces in the browser. In other words, you can compose music by writing some JavaScript Code. People using it are making some really great music. You can check some examples here https://strudel.cc/intro/showcase/
Thanks for reading!
Add a comment
Comments (0)
Copyright © 2025 Abderrahmane Faiz
